long short trading strategy neutral

Stretch-Short Fairness Strategy using Ranking: : Simple Trading Strategies Part 4

In the last post, we covered Pairs trading strategy and demonstrated how to leverage information and mathematical analysis to create and automate a trading scheme.

Long-Short Equity Scheme is a born extension of Pairs Trading applied to a handbasket of stocks.

Download Ipython Notebook here.

Underlying Principle

Long-life-Short equity strategy is both long and short stocks simultaneously in the securities industry. Only like pairs trading identifies which stock is tacky and which is expensive in a pair, a Long-Short strategy will rank all stocks in a basket to identify which stocks are relatively cheap and costly. Information technology bequeath then go lengthened (buys) the top n equities supported the ranking, and short (sells) the bottom n for equal amounts of money(Total value of long set = Total value of short-stalked position).

Remember how we same that Pairs Trading is a market neutral strategy? So is a Long-Short strategy as the equal turnover long and short positions ensure that the strategy will remain market unreactive (immune to market movements). The scheme is likewise statistically robust — by ranking stocks and entering multiple positions, you are making many another bets on your ranking model rather than just a few risky bets. You are also betting purely on the quality of your ranking scheme.

What is a Ranking Scheme?

A ranking scheme is any model that can assign each stock a enumerate supported on how they are expected to execute, where higher is better or worse. Examples could be treasure factors, field indicators, pricing models, or a combination of all of the above. E.g., you could use a impulse indicator to give a superior to a basket of trend following stocks: stocks with highest momentum are expected to continue to exercise well and buzz off the highest ranks; stocks with lowest momentum testament do the rack up and get last-place rans.

The winner of this scheme lies just about entirely in the ranking scheme used — the better your ranking connive can separate high performing stocks from low performing stocks, healthier the returns of a prolonged-deficient equity strategy. Information technology automatically follows that developing a ranking dodging is nontrivial.

What happens at one time you have a Ranking Scheme?

At one time we have determined a senior dodge, we would apparently like to be able to profit from information technology. We do this aside investing an equal sum into purchasing stocks at the top of the ranking, and selling stocks at the bottom. This ensures that the strategy will make money proportionately to the quality of the ranking only, and will be market colourless.

Permit's say you are superior m equities, have n dollars to invest, and want to hold a total of 2p positions (where m dangt; 2p ). If the stock at rank 1 is expected to perform the pip and old-hat at rank and file m is expected to do the C. H. Best:

You take the stocks in position 1,…,p in the ranking, deal n/2p dollars deserving of all stock
For each stock in position m−p,…,m in the ranking, buy n/2p dollars worth of each stock

Note: Friction Because of Prices Because stock prices wish not always divide n/2p evenly, and stocks must be bought in integer amounts, there will be some imprecision and the algorithm should get every bit imminent as it can to this number. For a strategy functional with n=100000 and p=500, we see that

n/2p=100000/1000 =100

This will cause handsome problems for stocks with prices dangt; 100 since you can't buy fractional stock. This is alleviated by trading fewer equities or increasing the Capital.

Let's work through a hypothetical example

We generate random stock name calling and a unselected factor on which to rank and file them. Let's also assume our future returns are actually contingent these factor values.

          importee numpy as Np
import statsmodels.api as Master of Science
import scipy.stats as stats
import scipy
implication matplotlib.pyplot as plt
importation seaborn as sns
importation pandas as pd          ## Job SETUP ##          # Generate stocks and a hit-or-miss component value for them          stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)          # Generate future returns for these are contingent our agent values
future_returns = current_factor_values + np.stochastic.normal(0, 1, 10000)          # Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

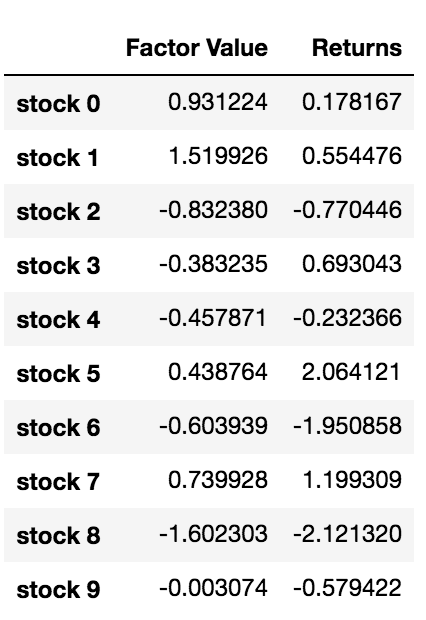
Now that we have factor out values and returns, we can see what would happen if we graded our equities based on element values, and then entered the mindful and telescoped positions.

          # Rank stocks
ranked_data = information.sort_values('Agent Value')          # Figure out the returns of for each one basket with a basket sizing 500, so gross (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)          for i in range(number_of_baskets):
            commence = i * 500
            end = i * 500 + 500            
            basket_returns[i] = ranked_data[start:end]['Returns'].mean()          # Plot of ground the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of All Basket'])
plt.display()

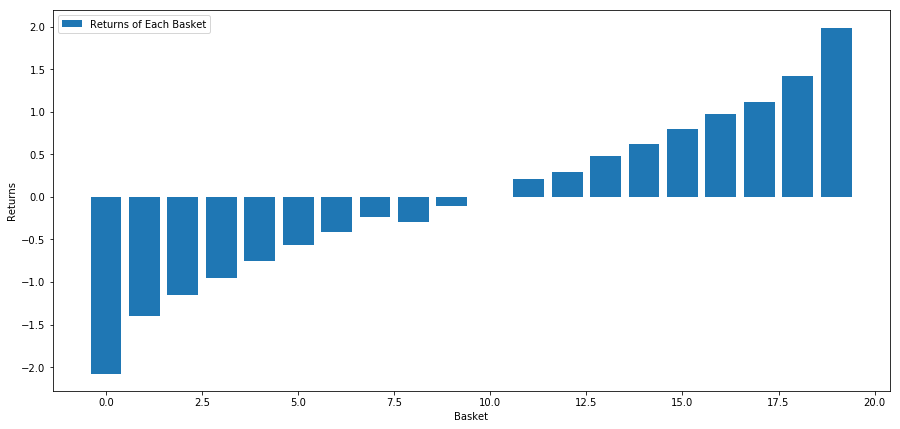
Our strategy is to sell the hoop at rank 1 and bribe the basket at rank 10. The returns of this strategy are:

          basket_returns[number_of_baskets-1]            -            basket_returns[0]

4.172

We're basically putting our money happening our ranking mould being able to separate and paste high performing stocks from low performing stocks.

For the relaxation of this post, we'll talk of how to evaluate a superior scheme. The nice thing about making money based on the spread of the ranking is that it is unaffected by what the market does.

Let's consider a real world example.

We load data for 32 stocks from distinguishable sectors in Sdanamp;P500 and try to downright them.

          from backtester.dataSource.yahoo_data_source moment YahooStockDataSource
from datetime import datetime          startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
            'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
            'HD','LOW','KO','LLY','MCD','MET','NEM',
            'PEP','PG','M','SWN','T','TGT',
            'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
            dataSetId=dataSetId,
            instrumentIds=instrumentIds,
            startDateStr=startDateStr,
            endDateStr=endDateStr,
            result='history')          price = 'adjClose'

Let's start by using incomparable month normalized impulse as a ranking indicator

          ## Specify normalized momentum
def momentum(dataDf, catamenia):
            restitution dataDf.sub(dataDf.shift(time period), fill_value=0) / dataDf.iloc[-1]          ## Lading at issue prices in a dataframe
information = ds.getBookDataByFeature()['Adj Close']          #Let's load up momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

At present we're departure to analyze our stock behavior and see how our universe of stocks work w.r.t our selected ranking ingredien.

Analyzing information

Gillyflower behavior

We look at how our chosen hoop of stocks acquit w.r.t our ranking model. To do this, let's calculate one workweek forward return for whol stocks. And then we bottom look at the correlation coefficient of 1 week guardant return with previous 30 24-hour interval momentum for every stock. Stocks that exhibit undeniable correlation are slue following and stocks that exhibit negative correlation are stingy reverting.

          # Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = Trustworthy)          # Calculate correlations between impulse and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])          mscores = mscores[mscores.index.isin(returns.index)]          for i in correlations.index:
            grudge, pvalue = stats.spearmanr(mscores[i], returns[i])
            correlations['pvalues'].loc[i] = pvalue
            correlations['Scores'].loc[i] = seduce
correlations.dropna(inplace = True)
correlations.sort_values('Lashing', inplace=Legitimate)          l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.fable(['Correlation over Totally Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-Day forward returns by Stock'%(day,forward_return_day));
plt.show()

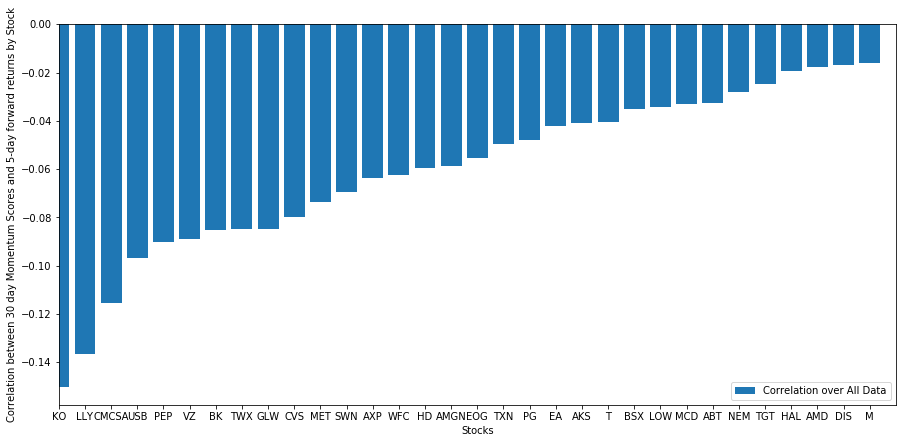
All our stocks are mean reverting to some academic degree! (Plainly we choose the universe to cost this way :) ) This tells us that if a stock ranks high connected momentum score, we should gestate it to execute poorly following calendar week.

Correlativity between Ranking referable Impulse Grade and Returns

Next, we need to smel at correlativity 'tween our senior score and forward returns of our universe, i.e. how predictive of of forward returns is our higher-ranking factor? Does a high relative crying predict destitute relative returns or vice versa?

To ut this, we estimate daily correlativity between 30 twenty-four hours impulse and 1 week forward returns of complete stocks.

          correl_scores = pd.DataFrame(index = returns.indicator.intersection(mscores.index), columns = ['Scores', 'pvalues'])          for i in correl_scores.index:
            score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
            correl_scores['pvalues'].loc[i] = pvalue
            correl_scores['Scores'].loc[i] = sexual conquest
correl_scores.dropna(inplace = True)          l = correl_scores.index number.size
plt.number(figsize=(15,7))
plt.bar(reach(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scads']), 1,l+1, colors='r', linestyles='dotted')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Bastardly Correlation over All Information', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation betwixt %s day Impulse Scores and %s-day forward returns'%(day,forward_return_day));
plt.demonstrate()

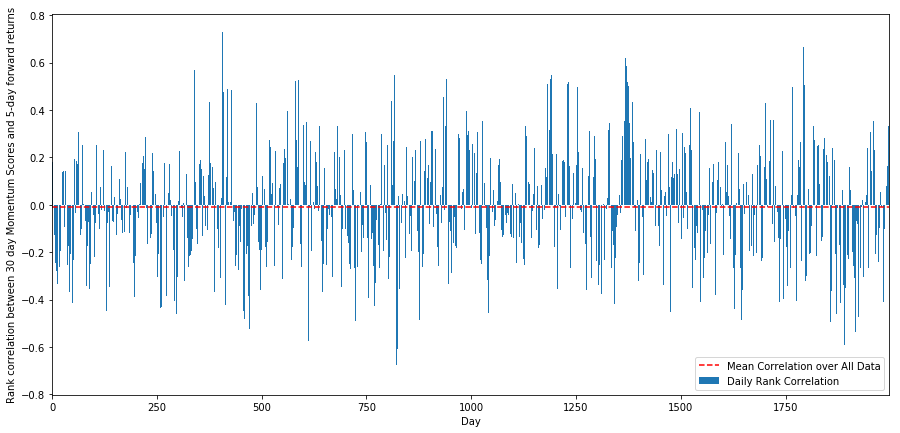
Daily Correlation coefficient is quite noisy, but very slightly negative (This is expected, since we said all the stocks are mean reversion). Rent out's too take average monthly correlation of scores with 1 month forward returns.

          monthly_mean_correl =correl_scores['Heaps'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colours='r', linestyles='dotted')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Coefficient of correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Absolute coefficient of correlation betwixt %s day Momentum Scores and %s-day forrad returns'%(day,forward_return_day));
plt.show()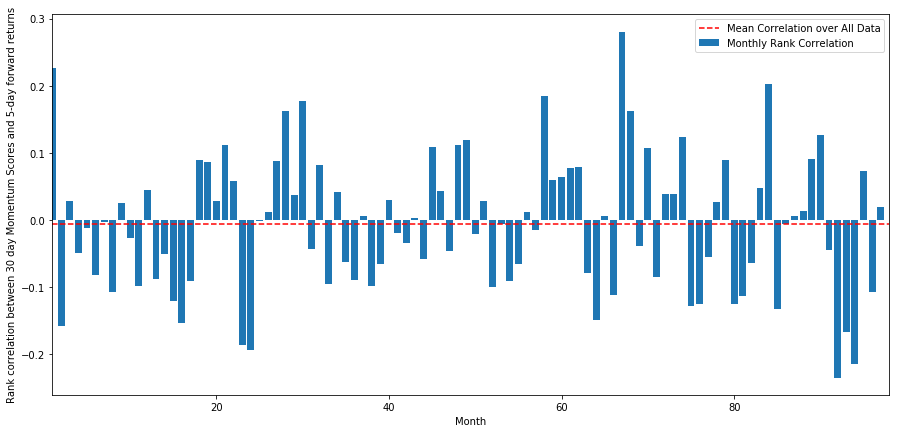

We can view that the average correlation is somewhat negative again, but varies much day-after-day arsenic well from month to month.

Average Basket Coming back

Now we compute the returns of baskets taken out of our ranking. If we membership whol equities and then split them into nn groups, what would the ungenerous return follow of each group?

The 1st step is to create a routine that will give us the mean reappearance in each field goal in a given the month and a ranking factor.

          def compute_basket_returns(factor, forward_returns, number_of_baskets, index):          data = atomic number 46.concat([factor.loc[index],forward_returns.loc[index]], bloc=1)
            # Rank the equities happening the ingredien values
            data.columns = ['Factor Value', 'Headlong Returns']
            information.sort_values('Factor Value', inplace=Admittedly)
            # How many equities per basket
            equities_per_basket = np.stun(len(data.index) / number_of_baskets)          basket_returns = np.zeros(number_of_baskets)          # Reckon the returns of apiece basketball hoop
            for i in range(number_of_baskets):
            start = i * equities_per_basket
            if i == number_of_baskets - 1:
            # Handle having a few extra in the go basket when our number of equities doesn't divide well
            end = len(data.index number) - 1
            else:
            end = i * equities_per_basket + equities_per_basket
            # Actually reckon the mean returns for each basket
            #s = data.index number.iloc[start]
            #e = data.index.iloc[end]
            basket_returns[i] = information.iloc[int(start):int(end)]['Cheeky Returns'].mean()                  return basket_returns

We cipher the ordinary return of each basket when equities are ranked based along this score. This should spring us a sense of the relationship over a lifelong timeframe.

          number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(drift).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = Genuine)          for m in forward_returns.index.intersection(resampled_scores.index):
            basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
            mean_basket_returns += basket_returns          mean_basket_returns /= l            
print(mean_basket_returns)
# Game the returns of each handbasket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

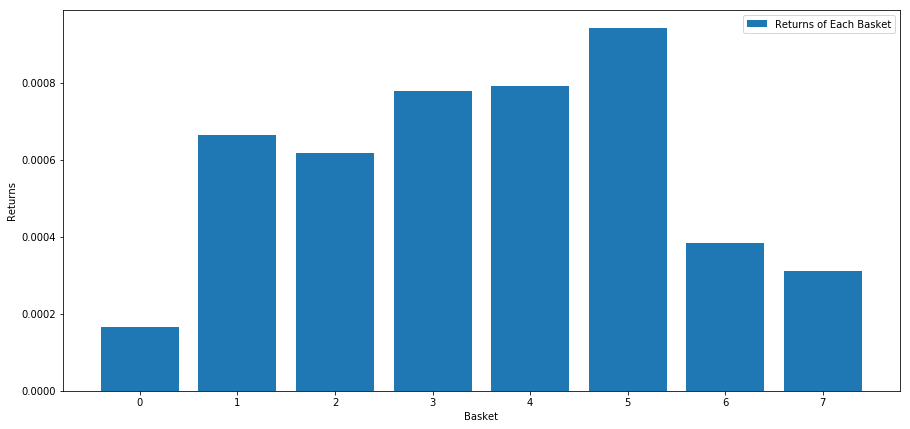
Seems like we are capable to separate high performers from low performers with very small achiever.

Spread Consistency

Of naturally, that's just the average relationship. To get a sense of how consistent this is, and whether or non we would neediness to trade on information technology, we should look at it over time. Here we'll take the monthly spreads for the starting time two years. We can see a dish out of variation, and further analysis should be done to determine whether this momentum score is tradeable.

          total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
            temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[calendar month]]
            temp_scores = resampled_scores.loc[monthly_index[calendar month-1]:monthly_index[month]]
            for m in temp_returns.indicant.intersection(temp_scores.index):
            basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
            mean_basket_returns += basket_returns                  strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
                              mean_basket_returns /= temp_returns.index.carrefour(temp_scores.index).size
                              r = int(np.floor((calendar month-1) / 6))
              c = (month-1) % 6
              axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
              axarr[r, c].xaxis.set_visible(False)
              axarr[r, c].set_title('Month ' + str(month))
plt.prove()

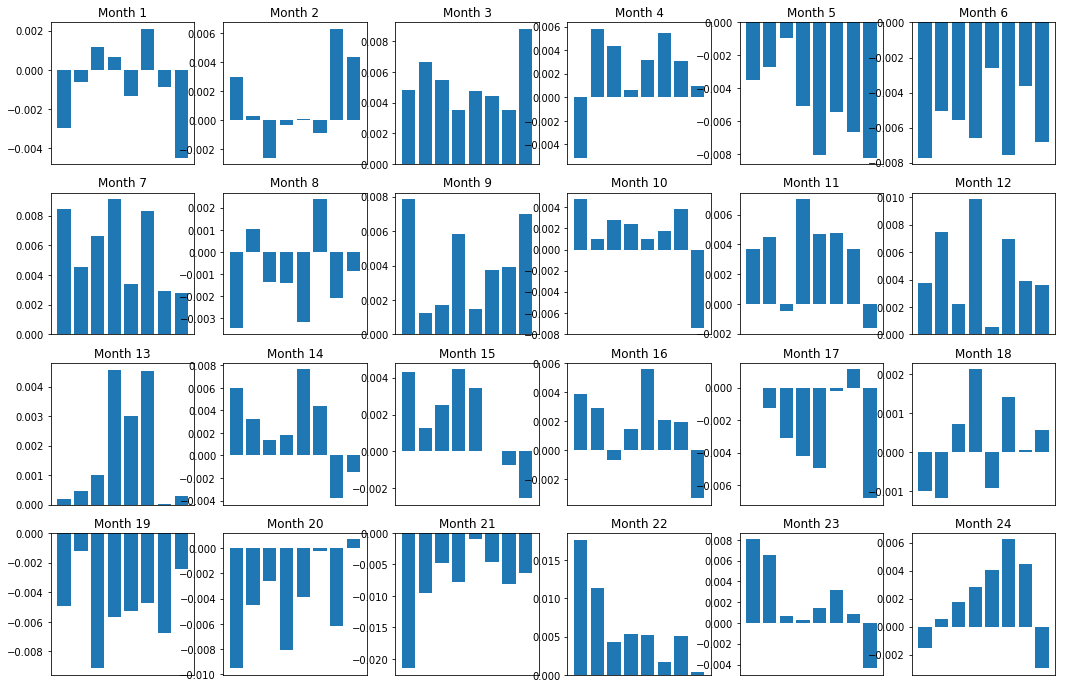
          plt.figure(figsize=(15,7))
plt.plat(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.caption(['Monthly Strategy Returns','Cumulative Strategy Returns'])
plt.show()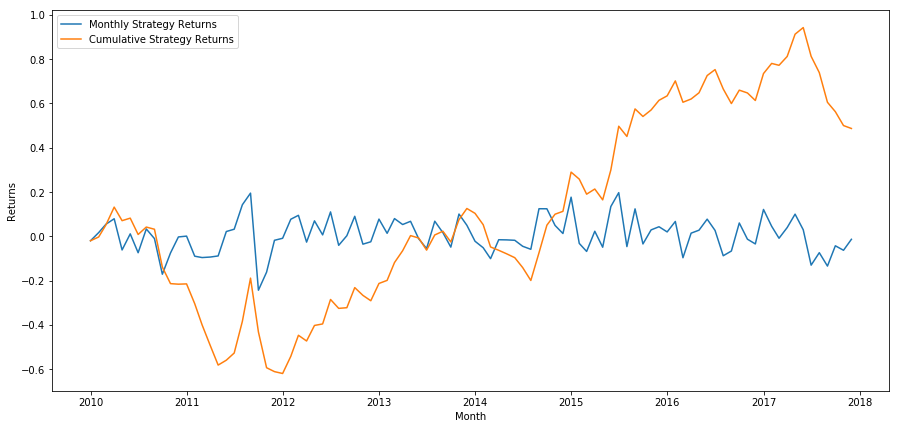

Finally, lets view the returns if we had bought the last basket and sold the first basket each month (assumptive equal uppercase allotment to each security)

          total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Annual Returns: 5.03%

We see that we have a very faint ranking scheme that only mildly separates high performing stocks from under playing stocks. Besides, this ranking intrigue has none consistency and varies a lot calendar month to month.

Determination the correct ranking connive

To execute a long-short equity, you efficaciously exclusively have to determine the ranking scheme. Everything after that is mechanical. Once you have one long-short equity strategy, you can swap in different ranking schemes and leave everything other in range. IT's a precise convenient direction to quick reiterate over ideas you have without having to worry about tweaking code every time.

The superior schemes can come from jolly much any model as wellspring. IT doesn't have to be a apprais based gene model, it could be a machine eruditeness technique that predicted returns nonpareil-calendar month forrade and hierarchal based on that.

Choice and Evaluation of a Higher-ranking Scheme

The ranking scheme is where a long-close equity scheme gets its edge, and is the most of the essence component. Choosing a right ranking scheme is the stallion trick, and there is nobelium easy answer.

A good starting bespeak is to pick existing known techniques, and see if you can change them slightly to get increased returns. We'll discuss a few protrusive points here:

Clone and Tweak: Choose one that is commonly discussed and see if you can modify it slightly to get ahead back an edge. Often multiplication factors that are unexclusive wish have no signalise left as they have been completely arbitraged out of the market. However, sometimes they contribute you in the word-perfect direction of where to go on.
Pricing Models: Any model that predicts future returns can equal a factor. The future return predicted is now that factor, and can be old to rank your universe. You can take any complicated pricing exemplary and transform it into a ranking.
Price Based Factors (Technical Indicators): Price based factors, wish we discussed today, take information about the liberal arts price of each fairness and use it to generate the factor value. Examples could be moving average measures, impulse ribbons, or volatility measures.
Reversion vs. Impulse: It's important to note that some factors bet that prices, once moving in a direction, will continue to do so. Some factors bet the opposite. Both are valid models on variant prison term horizons and assets, and information technology's important to investigate whether the underlying behavior is momentum or reversion based.
Fundamental Factors (Respect Based): This is using combinations of fundamental values like P.E ratio, dividend etc. Fundamental values hold in information that is united to concrete humankind facts about a company, thusly in many ways can be more beefy than prices.

At last, developing predictive factors is an coat of arms race in which you are trying to appease unrivalled step forwards. Factors get arbitraged out of markets and let a life, so it's important that you are constantly doing employment to determine how a great deal decay your factors are experiencing, and what new factors might be accustomed take their place.

Additional Considerations

Rebalancing Frequency

Every ranking system will be predictive of returns over a somewhat different timeframe. A price-founded mean lapsing may glucinium predictive complete a some years, spell a assess-based factor model may Be predictive over many months. It is important to determine the timeframe over which your model should be predictive, and statistically swear that before capital punishment your strategy. You don't want to overfit aside trying to optimize the rebalancing frequency — you will inevitably find one that is arbitrarily better than others, but non necessary because of anything in your model. One time you have determined the timeframe happening which your ranking dodging is prophetical, try to rebalance at nigh that frequency so you're taking engorged advantage of your models.

Capital Capacity and Transaction Costs

Every strategy has a stripped-down and maximum amount of capital it can trade before it boodle being profitable. The minimum threshold is usually set away dealings costs.

Trading many equities will termination in high transaction costs. Suppose that you lack to leverage 1000 equities, you will obtain a few thousand dollars in costs per rebalance. Your upper-case letter base must be high sufficiency that the transaction costs are a small percentage of the returns being generated by your scheme. For example, if your capital is 100,000$ and your strategy makes 1% per month(1000$) , then all of these returns will Be embezzled up by transaction costs.. You would want to be running the strategy along millions of dollars for it to be productive over 1000 equities.

The minimum capacity is quite high as such, and dependent largely on the number of equities traded. However, the maximum capacity is also incredibly high, with seven-day-short fairness strategies capable of trading hundreds of millions of dollars without losing their edge. This is true because the strategy rebalances relatively infrequently, and the add u dollar volume is divided by the number of equities listed. Therefore dollar-volume per equity is quite a low and you wear't have to worry about impacting the market by your trades. Let's say you're trading 1000 equities with 100,000,000$. If you rebalance your entire portfolio every month, you are entirely trading 100,000 dollar-volume per month for apiece equity, which isn't enough to be a significant market share for most securities.